The Lagrange interpolating polynomial is simply a reformulation of the Newton polynomial
that avoids the computation of divided differences. It can be represented concisely as
where
where Π designates the “product of.” For example, the linear version (n = 1) is
and the second-order version is
Consequently, the summation of all the products designated by first equation is the unique nthorder
polynomial that passes exactly through all n + 1 data points.
Reference; Numerical Methods for Engineers. Steven C. Chapra and Raymond P. Canale
public static void main (String[] args)
{
//Lagrange Polynomial
double[] x= new double[] {1,4,6};
double[] y= new double[] {0,1.386294,1.791760};
int n,grade;
double xval,sum, product;
xval=2;
sum=0;
grade=2;
n=grade+1;
for (int i=0; i<n; i++){
product=y[i];
for (int j=0; j<n; j++){
if(i!=j){
product=product*(xval-x[j])/(x[i]-x[j]);
}
}
sum=sum+product;
}
System.out.println(sum);
}
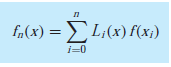



No hay comentarios:
Publicar un comentario